一、实验目的
1.测定金属材料的E和并验证虎克定律。
2.学习掌握电测法的原理和电阻应变仪的操作。
二、实验原理
板试样的布片方案如图8-1所示。在试样中部截面上，沿正反两侧分别对称地布有一对轴向片R和一对横向片Rˊ。试样受拉时轴向片R的电阻变化为R，相应的轴向应变为p与此同时横向片因试样收缩而产生横向应变为ˊ。E与的测试方法如下：
E的测试
在线弹性范围内E=
代表-曲线直线部分的斜率。由于试验装置和安装初始状态的不稳定性。拉伸曲线的初始阶段往往是非线性的。为了减少测量误差，试验宜从初载P0开始, P0≠0,与P0对应的应变仪读数εp可预调到零,也可设定一个初读数,而E可通过下式测定(图8-2),即
P0为试验的末载荷,为保证模型试验的安全,试验的最大载荷Pmax应在试验前按同类材料的弹性极限σc进行估算, Pmax应使σmax＜ 80%σc.
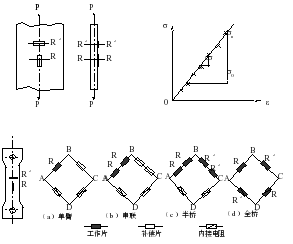
图8-1 板试件布片方案 图8-2 E的测定
图8-3 几种不同的组桥方式
为验证虎克定律,载荷由P0到Pn可进行分级加载,
,其中Pn＜Pmax.每增加一个ΔP,即记录一个相应的应变读数,检验ε的增长是否符合线性规律.用上述板试样测E,合理地选择组桥方式可有效地提高测试灵敏度和试验效率.下面讨论几种常见的组桥方式。
单臂测量（图8-3a）
试验时，在一定载荷条件下，分别对前、后两枚轴向应变片进行单片测量，并取其平均值 
。显然（
）即代表载荷在（Pn-P0）作用下试样的实际应变量。而且
消除了偏心弯曲引起的测量误差。
轴向片串联后的单臂测量（图8-3b）
为消除偏心弯曲的影响，可将前后轴向片串联后接在同一桥臂（AB）上，而相邻臂（BC）接相同阻值的补偿片。受拉两轴向片的电阻变化分别为
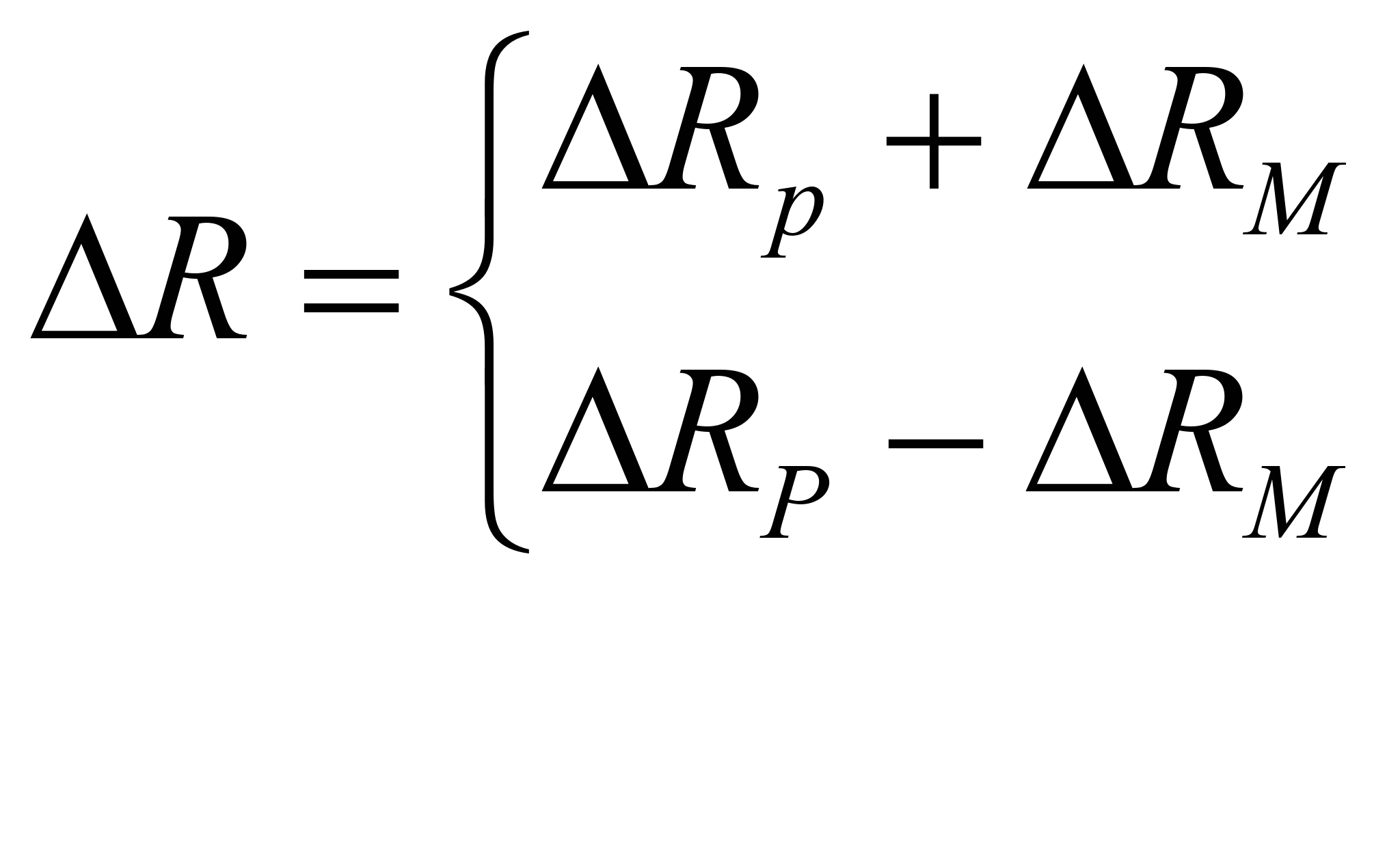（8-1）
ΔRM为偏心弯曲引起的电阻变化，拉、压两侧大小相等方向相反，根据桥路原理AB臂有：
因此轴向片串联后，偏心弯矩的影响自动消除，而应变仪的读数就等于试样的应变即ε仪=εp,显然测量灵敏度没有提高。
串联后的半桥测量（图8-3C）
若两轴向片串联后接AB；两横向片串联后接BC，偏心弯曲的影响可自动消除，而且温度可自动补偿。根据桥路原理得知。
其中ε1=εp；ε2=-μεp，εp轴向应变，μ为材料的泊桑比。由于ε3，ε4为零，故
（8-2）
即输出电压是单臂工作的（1+μ）倍，即
（8-3）
而
（8-4）
如果材料的泊桑比已知，这种组桥方式测量灵敏度提高（1+μ）倍。
全桥测量（图8-3d）
按图3-12d的方式组桥进行全桥测量，不仅消除了偏心和温度的影响，而且输出电压是单臂测量的2（1+μ）倍即：
（8-5）
测量灵敏度比单臂工作时提高2（1+μ）倍。
2．μ的测试
利用试样的横向片和轴向片合理组桥：在设定载荷下分别测定试样的横向应变ε′和轴向应变εp并随时检验其增长是否附合线性规律，测出一组ε′和εp值，即可确定μ值。
三、实验设备
1.5吨万能试验机；电阻应变仪；板试样试验装置
（五）试件：
平板试件多用于电测法，试件形状及贴片方位如 图8-1所示。为了保证拉伸时的同心度，通常在试件两端开孔，以销钉与拉伸夹头连接，同时可在试件正反面贴应变片，以提高试验结果的准确性。
（八）实验数据处理
用方格纸做出弹性阶段的σ-ε和ε′-ε曲线。将每个试验点都点在图上，然后拟合成直线，并注意原点位置的修正。
采用最小二乘法数值分析法，确定E和 μ的数值。
完成试验报告、报告应按即定格式书写，各类数据必须用表格系统地整理出来。
参考表格：
试验次数
载荷
（KN）
应变数（με）
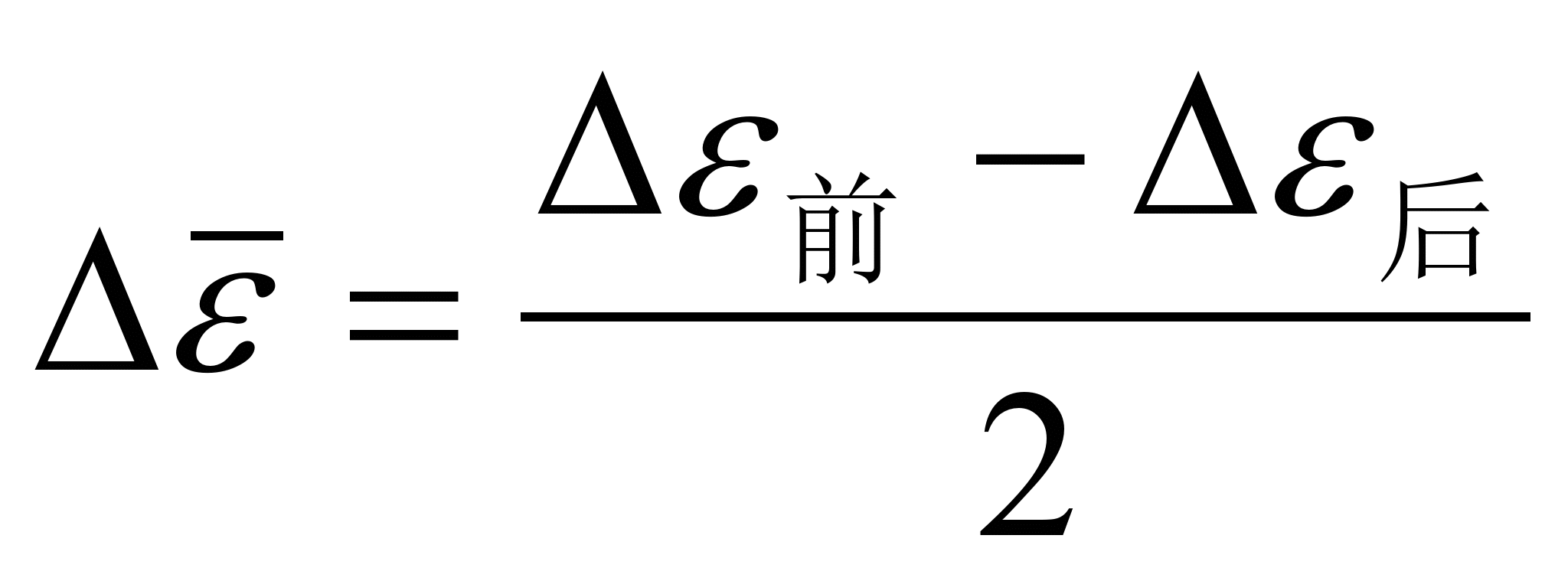
（με）
ε前
Δε前
ε后
Δε后
1
P1
P2
P3
P4
2
P1
P2
P3
P4